What with the COVID19 related confinement, I have been playing a lot of board games on board game arena with friends, colleagues, you name it. When you first create an account, the site takes you through the tutorial of a simple probabilistic risk vs gain evaluation game called Can’t Stop. Having a little more time on my hands during weekends than usual, I decided to train a reinforcement learning agent to learn to play this game, for which the full code can be found here.

Can’t Stop!

The easiest way to understand the mechanics of the game if you don’t already know it is probably to watch this tutorial. Briefly though, the set up is as follows. This 2 to 4-player game comprises of 11 columns running from 2 to 12, and the goal is to be the first to claim three columns, which is done by moving your counter from the bottom to the top of the column. As can be seen, the columns are of different heights, but this is compensated by the probability of being able to move up each column.

At each turn, the players roll 4 dice and choose columns corresponding to the result when they separate the dice into two pairs and sum each pair. After choosing his columns, the player then decides whether to end his turn or continue rolling. The catch is that in any turn, a player can move up a maximum of three different columns, and loses all advances made should he perform a roll where he is unable to advance on any of the three columns of that turn. Players therefore aim to stop and lock in their positions on these columns at the optimal moment. For every subsequent turn, previous locked in advances are kept, and players can choose new columns to move up.

The game therefore involves balancing the risk and reward of continuing to roll, with some subtleties in the multi-player dynamic that involve whether columns where other players have already established a headstart are worth pursuing.

Reinforcement Learning

With the stunning victory of AlphaGo over Lee Sedol in the game of Go, long thought to be a benchmark in the development of artificial intelligence, it seems as though everyone in the machine learning community was talking about reinforcement learning, especially with respect to games with well defined rules. As reinforcement learning has already been explained much more capably elsewhere, and I will give only a brief summary here.

The idea behind this branch of machine learning is actually simple. Just as a child learns to avoid hot objects after experiencing the pain of burning, or to reach for sweets because he remembers the pleasure from eating it, the idea is to train an algorithm with punishments and rewards so it knows how to react to an environment optimally. Some terms generally used in setting up a problem to solve in reinforcement learning:

The agent is the algorithm we train, who will take actions in an environment, whose state will change as a result of the action. In classical reinforcement learning, the agent then receive the following information about this change: an observation of the state (which might not necessarily contain all the information present in the state) and a reward for the action taken given the original observation. The agent then takes the next action, and the cycle repeats. Over time, as the agent collects a history of the observations and rewards resulting from its different actions, it should learn to perform the correct actions upon receiving an observation of the state.

In general, the agent does not need to know anything about the game he is playing beforehand, nor observe human players playing the game. In the example of Go, the algorithm would probably choose positions on the board completely randomly at the start, then learn over time how to surround territory, leading to different strategies and moves, as well as a final victory at the end of the game. The beauty of the reinforcement learning is that the agent learns to associate the rewards not only with the last action taken, but also with the whole history of actions and observations that lead to this point. This means that the agent can learn to associate long term rewards with actions that might be potentially bring less reward at the moment (as an analogy, we can choose to suffer the brief pain of exercise and not indulge in the pleasures of junk food, in exchange for good health in the long term.)

Deep Q Network

The DQN agent is used where action choices are discrete and the number of possible actions is fixed and finite. It basically works as follows: we train a neural network that outputs a “score” for each of the possible choices of actions given an observation. The agent then chooses the action to take based on these scores - when using this agent in practice, it should always choose the action with the best score, if still in training, it might at times choose an action with smaller scores in case it might lead to future actions with higher scores. Different ways of choosing an action can be decided based on how we want to prioritize exploration vs exploitation - whether we want to exploit the actions we already know are good, or to explore more in case there are better options.

(The name deep Q network comes from the deep neural network involved, and the reward function Q it tries to approximate, that takes into account future possible evolutions of the actions and not merely the current resulting reward.)

Details on Implementation

This section will contain rather technical details on implementation choices (although it should be generally understandable by non-technical readers), so feel free to skip ahead to the “Results” section for a video of a game played by the trained agents instead!

Agent

I decided to use the Keras RL implementation of a DQN agent to learn to play the game, mostly due to pre-existing familiarity with this project. As Keras RL doesn’t support multi-player environments out of the box, I adapted the Interleaved Agent as developed by velochy, which allow the different agents to learn to play together, and to be decoupled from each other at the end.

As this is a multi-phase game on top of being a multi-player game, I chose to use the same agent to take actions in both the “stop or continue” and “choose which dice pair” phases to simplify training. This means that not only does the agent have to learn how to complete the game without knowing the rules of the game, it also has to learn how to respond correctly to the phase - the agent cannot choose to “stop or continue” when it is in the “choose which dice pair” phase and vice versa, otherwise he receives a penalty and the game would end. In addition, unlike human beings who are able to infer patterns from a wider understanding of the world, the agent has no visual or pattern relating clues - it does not know it is playing a board game with logical rules, cannot observe the design of the board and summise that choosing a pair of dice that sum to 7 corresponds to moving up the column 7, therefore this pattern should hold true for other sums and columns.

Practically, the agent will choose an action corresponding to the numbers 0 to 7, with 0 and 1 representing stopping and continuing, and 2-7 representing the 6 possible choices of die sums. If the player chooses a die sum and the other die sum in the pair is still feasible (such as at the start of the turn when the player has yet to advance on any column), both die sums will be played (that is, choosing 2 or 3 would be equivalent when both die sums represented by 2 and 3 are feasible).

Alternatively, I don’t think that it would be too difficult to train two separate agents instead as the two phases are relatively independent, with one agent evaluating the risk of stopping and continuing, and the other agent choosing the optimal columns to continue. The interweaving of agent and environment forward and backward passes during training would require a more delicate adaptation, which is unlikely to be reusable in other environments though.

Environment

The environment I implemented uses Open AI’s Gym base environment class for compatibility with Keras RL’s training structure. The environment basically codes all of the rules of the games, including how it changes the state of the board after a player chooses an action, and how it generates dice rolls. The observations that the environment returns at each turn to the agent comprises of the following:

• the phase of the game (choose to stop or continue, choose dice pair)
• the positions of the player on each column of the board. The state of the current player is always placed first so that the four agents can interchangeably take the position of any player (since if we always return the four players’ positions in a fixed order, an agent trained as player 0 can only play optimally if it happens to be player 0 again).
• the positions of the other 3 players on the columns of the board. If less than 4 players are playing, the remaining empty slots are simply always 0. This allows for the same agent trained in a 4 player set up to play in games with 2 or 3 player as well.
• the three columns on which the player is advancing in this turn. Where less than three columns have been chosen, we fill the remaining places with 0s.

A sanity check on the implementation of anything probabilistic is always a good idea. We look at the histogram of the different dice sums generated over 100 games: (for each of the 6 possible choices per turn)

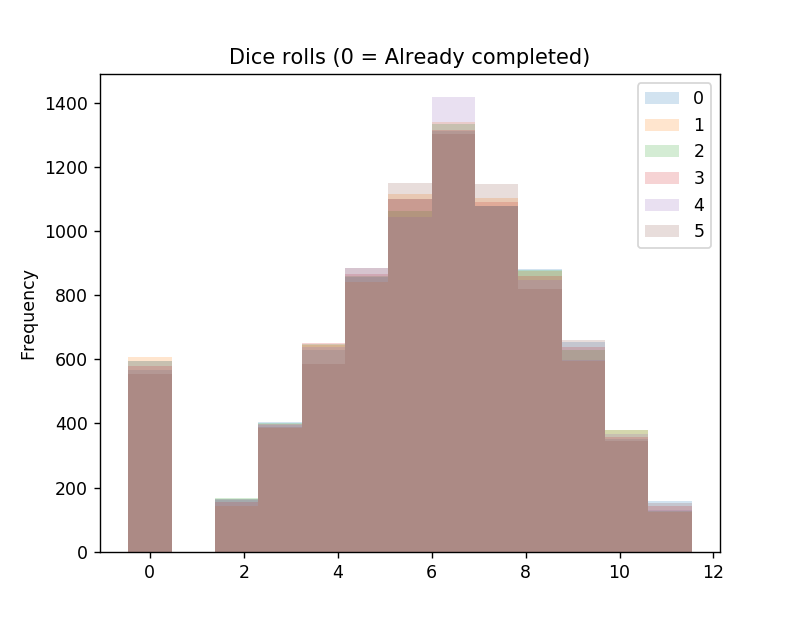
Everything looks as expected, which is a relief!

In theory, the only reward of this game comes at the end when the game is won. However, as I was also teaching my agents to choose the right actions corresponding to the right phases, the penalties associated with choosing the wrong actions for a given phase meant that the agent would first have to learn actions that result in zero penalties. I would think it possible to find the parameters allowing one to train agents on a “pure” version where the only reward is in winning three columns, but trying this out showed that practically speaking, the agents took too long to learn to move up the columns. I added in some partial rewards for completing a single column, and observed that agents then stopped immediately after performing one roll and thus advanced up the columns slowly, although a second roll is always non risky! In order to incentivize learning to advance multiple steps in a single turn, more partial rewards were given for when a player advances more in a single turn.

Results and Reflections

The results of a quick round of training over 100,000 steps already prove promising: the agents are able to complete the game and have learned to continue rolling the dice in most risk-free situations, although they rarely seem to like taking risks:

Although in general the agents appear to be taking logical options, we would have to implement some simple Keras callbacks to retrieve the actions taken by the agents over the testing phase in order to do analyze how well they actually are faring. We can for example look at the frequency of actions taken by all players in both phases over 100 games.

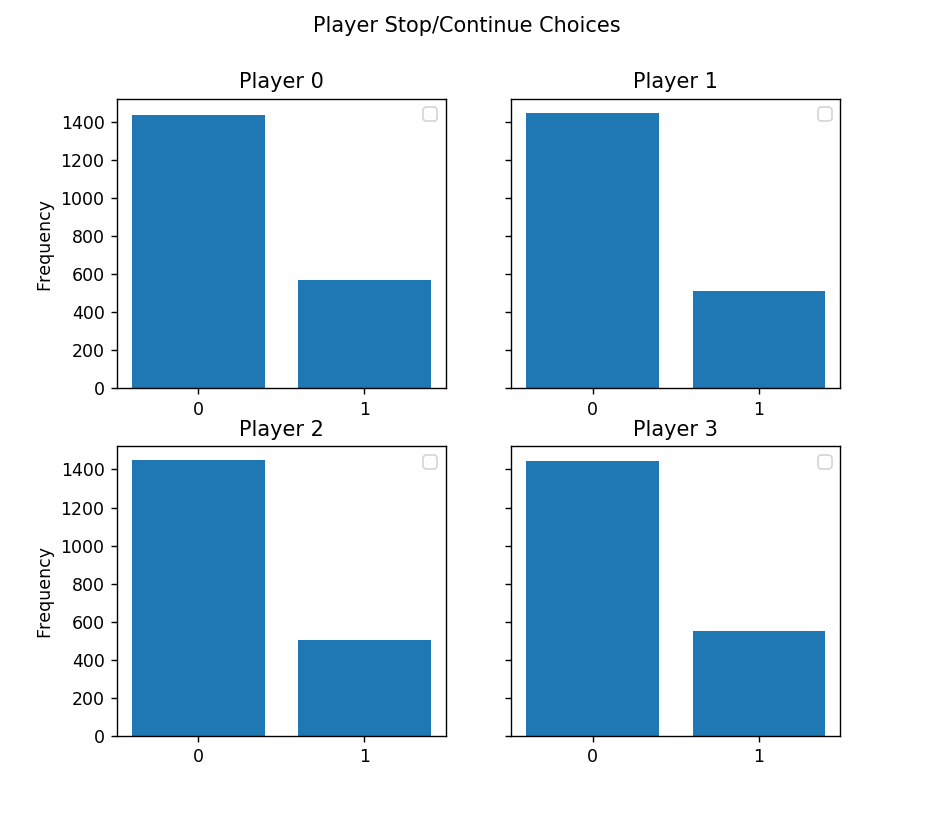
As can be seen for phase 0, where players choose whether to stop or continue, the players are stopping much more often than they are continuing. We can compare it to an absoultely risk free way of playing, which is when a player continues at least once before stopping each time it is his turn, and where the first two rolls result in less than three columns taken, choose again to continue. Thus in this risk free way of playing, the frequency of continuing should already by higher than or at least equal to the frequency of stopping - so our players are clearly not optimal here.

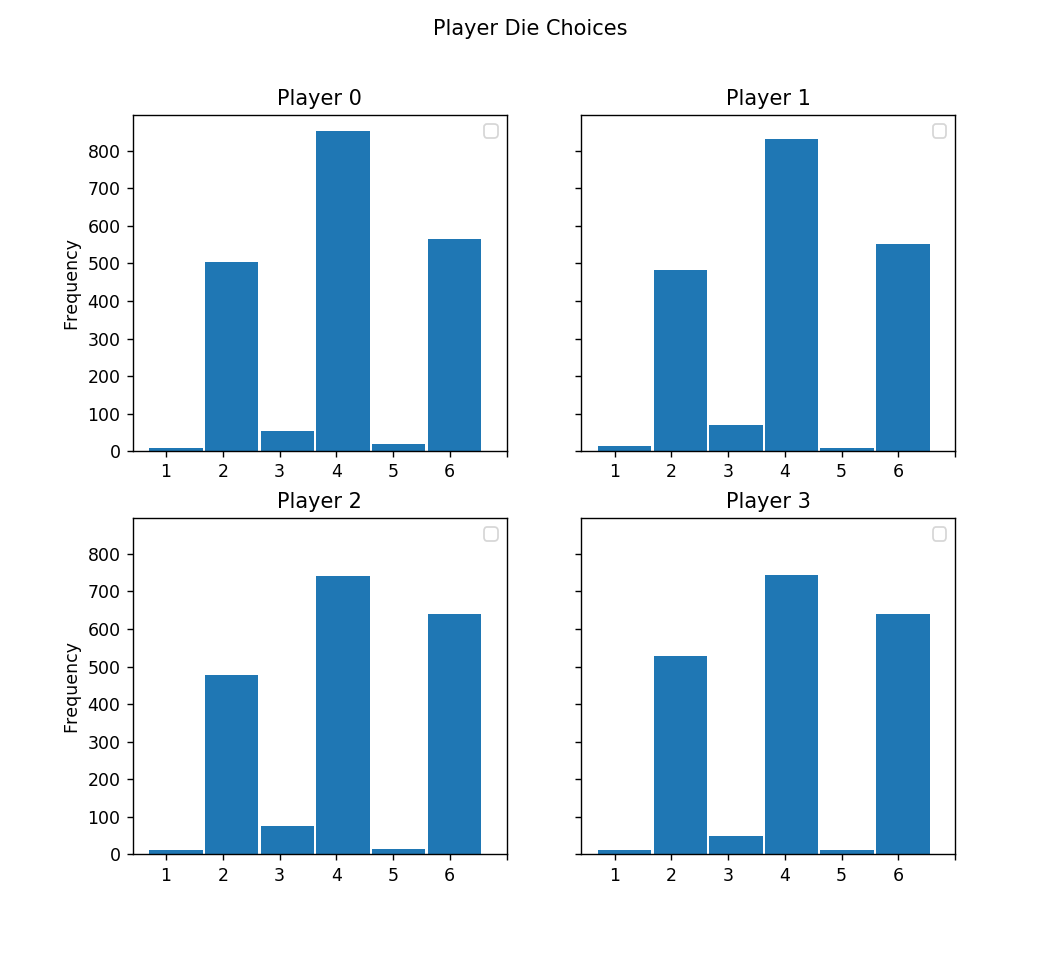
In phase 1, players choose a die sum. As a reminder, in my implementation, choosing one die sum when the other in the pair is feasible would result in both being selected, whereas when only one is feasible, only one will be selected. I would expect the players to choose equally all 6 possible actions as the optimal dice sum can appear in any of the six. That being said, this distribution is not surprising - since choosing any one of the pair is equivalent, specializing into one over the other in each pair is also a potentially optimal way to play. However, since the players are often stopping after one or two rolls, it is more likely that they too rarely see the scenario where they will have to choose only one of two actions, and so have not learned the distinction between choosing a pair and choosing just one of the two dice.

Further training did not yield better results, neither did some basic modification of the rewards structures. A better reward structure and optimized learning parameters of the agents might get the agents to yield more optimal (or at least different) results. I had thought that giving the largest reward to the agent who completed first would be incentive enough for agents to attempt to complete the fastest, but perhaps an added penalty per every extra time step taken could help induce faster conquest of columns.

Lastly, it could also be interesting to think of a way for the agents to share knowledge with each other. This would definitely allow for faster training, but might also allow for more complex strategies. In the current implementation, each agent is blind to the rolls and actions taken by other agents when it is not their turn, only observing the resulting board changes at the start of their turn. This is clearly different from human players being able to observe the strategies of the friends they are playing with (some people who prefer to go for the rare but easy to complete columns, 2 and 12) and adapt their own strategy accordingly.

Of course, since Can’t Stop is pretty straightforward probabilistically speaking, there’s no actual need to use reinforcement learning to create an AI to play the game, and a calculation of the expected gains conditioned on the board situation at each turn should yield a bot with decent performance. Still, this has been a fun side project!